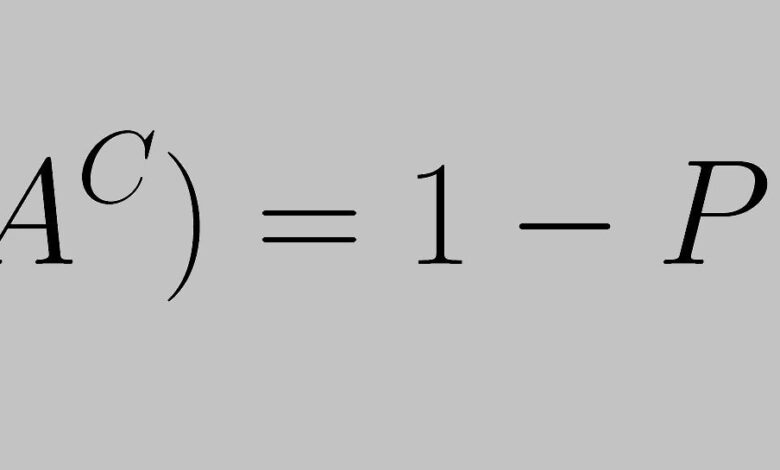
Contents
En statistique, la règle du complément est un théorème qui établit un lien entre la probabilité d’un événement et la probabilité du complément de l’événement de telle manière que si nous connaissons l’une de ces probabilités, nous connaissons automatiquement l’autre.
La règle du complément s’avère utile lorsque nous calculons certaines probabilités. Souvent, la probabilité d’un événement est compliquée ou compliquée à calculer, alors que la probabilité de son complément est beaucoup plus simple.
Avant de voir comment la règle du complément est utilisée, nous allons définir précisément ce qu’est cette règle. Nous commençons par un peu de notation. Le complément de l’événement A, constitué de tous les éléments de l’espace échantillon S qui ne sont pas des éléments de l’ensemble A, est désigné par AC.
Déclaration de la règle de complémentarité
La règle du complément est énoncée comme suit : « la somme de la probabilité d’un événement et de la probabilité de son complément est égale à 1 », comme l’exprime l’équation suivante :
P(AC) = 1 – P(A)
L’exemple suivant montre comment utiliser la règle du complément. Il deviendra évident que ce théorème accélérera et simplifiera les calculs de probabilité.
Probabilité sans la règle du complément
Supposons que nous jouions huit pièces de monnaie équitables. Quelle est la probabilité que nous ayons au moins une tête qui apparaisse ? Une façon de le savoir est de calculer les probabilités suivantes. Le dénominateur de chacune s’explique par le fait qu’il y a 28 = 256 résultats, chacun d’entre eux étant également probable. Tous les résultats suivants utilisent une formule de combinaison :
- La probabilité de retourner exactement une tête est de C(8,1)/256 = 8/256.
- La probabilité de renverser exactement deux têtes est de C(8,2)/256 = 28/256.
- La probabilité de renverser exactement trois têtes est de C(8,3)/256 = 56/256.
- La probabilité de renverser exactement quatre têtes est de C(8,4)/256 = 70/256.
- La probabilité de retourner exactement cinq têtes est de C(8,5)/256 = 56/256.
- La probabilité de renverser exactement six têtes est de C(8,6)/256 = 28/256.
- La probabilité de retourner exactement sept têtes est de C(8,7)/256 = 8/256.
- La probabilité de retourner exactement huit têtes est de C(8,8)/256 = 1/256.
Ces événements s’excluant mutuellement, nous additionnons les probabilités en utilisant la règle d’addition appropriée. Cela signifie que la probabilité que nous ayons au moins une tête est de 255 sur 256.
Utiliser la règle du complément pour simplifier les problèmes de probabilité
Nous calculons maintenant la même probabilité en utilisant la règle du complément. Le complément de l’événement « nous retournons au moins une tête » est l’événement « il n’y a pas de têtes ». Il y a une façon pour que cela se produise, ce qui nous donne la probabilité de 1/256. Nous utilisons la règle du complément et nous constatons que la probabilité souhaitée est de 1 moins 1 sur 256, ce qui est égal à 255 sur 256.
Cet exemple démontre non seulement l’utilité mais aussi la puissance de la règle du complément. Bien que notre calcul initial ne présente aucun problème, il était assez compliqué et nécessitait de multiples étapes. En revanche, lorsque nous avons utilisé la règle du complément pour ce problème, il n’y avait pas autant d’étapes où les calculs pouvaient mal tourner.