Définition et utilisation de l’Union en mathématiques

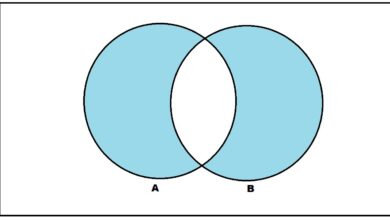
Une opération qui est fréquemment utilisée pour former de nouveaux ensembles à partir d’anciens est appelée l’union. Dans l’usage courant, le mot union signifie un rassemblement, comme les syndicats de travailleurs organisés ou le discours sur l’état de l’Union que le président des États-Unis prononce devant une session conjointe du Congrès. Au sens mathématique, l’union de deux ensembles conserve cette idée de rassemblement. Plus précisément, l’union de deux ensembles A et B est l’ensemble de tous les éléments x tels que x est un élément de l’ensemble A ou x est un élément de l’ensemble B. Le mot qui signifie que nous utilisons une union est le mot « ou ».

Le mot « ou »

Lorsque nous utilisons le mot « ou » dans les conversations quotidiennes, nous pouvons ne pas nous rendre compte que ce mot est utilisé de deux manières différentes. La manière est généralement déduite du contexte de la conversation. Si l’on vous demande « Voulez-vous le poulet ou le steak ? », il est généralement sous-entendu que vous pouvez avoir l’un ou l’autre, mais pas les deux. Comparez cela avec la question « Voulez-vous du beurre ou de la crème aigre sur votre pomme de terre au four ? » Ici, « ou » est utilisé dans le sens inclusif, c’est-à-dire que vous pourriez choisir uniquement du beurre, uniquement de la crème aigre, ou à la fois du beurre et de la crème aigre.

En mathématiques, le mot « ou » est utilisé au sens large. Ainsi, l’affirmation « x est un élément de A ou un élément de B » signifie que l’un des trois est possible :

• x est un élément de A seulement et non un élément de B
• x est un élément de B seulement et non un élément de A.
• x est un élément à la fois de A et de B. (On pourrait aussi dire que x est un élément de l’intersection de A et de B

Exemple

Pour un exemple de la façon dont l’union de deux ensembles forme un nouvel ensemble, considérons les ensembles A = {1, 2, 3, 4, 5} et B = {3, 4, 5, 6, 7, 8}. Pour trouver l’union de ces deux ensembles, nous énumérons simplement chaque élément que nous voyons, en prenant soin de ne pas en dupliquer d’autres. Les nombres 1, 2, 3, 4, 5, 6, 7, 8 se trouvent dans l’un ou l’autre ensemble, donc l’union de A et B est {1, 2, 3, 4, 5, 6, 7, 8 }.

Notation pour l’Union

En plus de comprendre les concepts relatifs aux opérations de la théorie des ensembles, il est important de pouvoir lire les symboles utilisés pour désigner ces opérations. Le symbole utilisé pour l’union des deux ensembles A et B est donné par A ∪ B. Une façon de se souvenir du symbole ∪ qui fait référence à l’union est de remarquer sa ressemblance avec un U majuscule, qui est l’abréviation du mot « union ». Attention, car le symbole de l’union est très similaire à celui de l’intersection. L’un est obtenu de l’autre par un retournement vertical.

Pour voir cette notation en action, reportez-vous à l’exemple ci-dessus. Ici, nous avions les ensembles A = {1, 2, 3, 4, 5} et B = {3, 4, 5, 6, 7, 8}. Nous écririons donc l’équation de l’ensemble A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8 }.

L’Union avec le jeu vide

Une identité de base qui implique l’union nous montre ce qui se passe lorsque nous prenons l’union de n’importe quel ensemble avec l’ensemble vide, désigné par le numéro 8709. L’ensemble vide est l’ensemble sans éléments. Ainsi, l’union de cet ensemble avec tout autre ensemble n’aura aucun effet. En d’autres termes, l’union de n’importe quel ensemble avec l’ensemble vide nous donnera l’ensemble original en retour

Cette identité devient encore plus compacte avec l’utilisation de notre notation. Nous avons l’identité : A ∪ ∅ = A.

Union avec l’ensemble universel

À l’autre extrême, que se passe-t-il lorsque nous examinons l’union d’un ensemble avec l’ensemble universel ? Comme l’ensemble universel contient tous les éléments, nous ne pouvons pas y ajouter quoi que ce soit. Donc l’union ou tout ensemble avec l’ensemble universel est l’ensemble universel.

Là encore, notre notation nous aide à exprimer cette identité dans un format plus compact. Pour tout ensemble A et l’ensemble universel U, A ∪ U = U.

Autres identités impliquant l’Union

Il existe beaucoup d’autres identités fixes qui impliquent l’utilisation de l’opération syndicale. Bien sûr, il est toujours bon de s’entraîner à utiliser le langage de la théorie des ensembles. Voici quelques-unes des plus importantes. Pour tous les ensembles A, et B et D, nous avons :

• Propriété réflexe : A ∪ A =A
• Propriété commutative : A ∪ B = B ∪ A
• Propriété associative : (A ∪ B) ∪ D =A ∪ (B ∪ D)
• Loi DeMorgan I : (A ∩ B)C = AC ∪ BC
• Loi DeMorgan II : (A ∪ B)C = AC ∩ BC