Contents
Le théorème de la limite centrale est un résultat de la théorie des probabilités. Ce théorème apparaît à plusieurs endroits dans le domaine des statistiques. Bien que le théorème de la limite centrale puisse sembler abstrait et dépourvu de toute application, ce théorème est en fait très important pour la pratique de la statistique.
Quelle est donc l’importance exacte du théorème de la limite centrale ? Tout est lié à la répartition de notre population. Ce théorème vous permet de simplifier les problèmes statistiques en vous permettant de travailler avec une distribution à peu près normale.
Déclaration du théorème
L’énoncé du théorème de la limite centrale peut sembler assez technique mais peut être compris si nous réfléchissons aux étapes suivantes. Nous commençons par un simple échantillon aléatoire de n individus appartenant à une population d’intérêt. À partir de cet échantillon, nous pouvons facilement former une moyenne d’échantillon qui correspond à la moyenne des mesures qui nous intéressent dans notre population.
Une distribution d’échantillonnage pour la moyenne de l’échantillon est produite en sélectionnant de manière répétée des échantillons aléatoires simples de la même population et de la même taille, puis en calculant la moyenne de l’échantillon pour chacun de ces échantillons. Ces échantillons doivent être considérés comme indépendants les uns des autres.
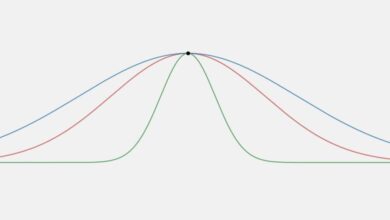
Le théorème limite central concerne la distribution de l’échantillon des moyennes de l’échantillon. On peut s’interroger sur la forme globale de la distribution de l’échantillonnage. Le théorème de la limite centrale indique que cette distribution d’échantillonnage est approximativement normale – communément appelée courbe en cloche. Cette approximation s’améliore à mesure que nous augmentons la taille des échantillons aléatoires simples qui sont utilisés pour produire la distribution de l’échantillonnage.
Il y a une caractéristique très surprenante concernant le théorème de la limite centrale. Le fait étonnant est que ce théorème dit qu’une distribution normale se produit indépendamment de la distribution initiale. Même si notre population présente une distribution asymétrique, ce qui se produit lorsque nous examinons des éléments tels que les revenus ou le poids des personnes, une distribution d’échantillonnage pour un échantillon de taille suffisamment importante sera normale.
Le théorème de la limite centrale en pratique
L’apparition inattendue d’une distribution normale à partir d’une distribution de population biaisée (même assez fortement biaisée) a des applications très importantes dans la pratique statistique. De nombreuses pratiques statistiques, telles que celles qui impliquent des tests d’hypothèses ou des intervalles de confiance, reposent sur des hypothèses concernant la population à partir de laquelle les données ont été obtenues. L’une des hypothèses initialement formulées dans un cours de statistique est que les populations avec lesquelles nous travaillons sont normalement réparties.
L’hypothèse selon laquelle les données proviennent d’une distribution normale simplifie les choses mais semble un peu irréaliste. Un petit travail sur des données réelles montre que les valeurs aberrantes, l’asymétrie, les pics multiples et l’asymétrie apparaissent assez régulièrement. Nous pouvons contourner le problème des données provenant d’une population qui n’est pas normale. L’utilisation d’une taille d’échantillon appropriée et le théorème de la limite centrale nous aident à contourner le problème des données provenant de populations qui ne sont pas normales.
Ainsi, même si nous ne connaissons pas la forme de la distribution d’où proviennent nos données, le théorème de la limite centrale dit que nous pouvons traiter la distribution d’échantillonnage comme si elle était normale. Bien sûr, pour que les conclusions du théorème soient valables, nous avons besoin d’un échantillon suffisamment grand. Une analyse exploratoire des données peut nous aider à déterminer la taille de l’échantillon nécessaire pour une situation donnée.