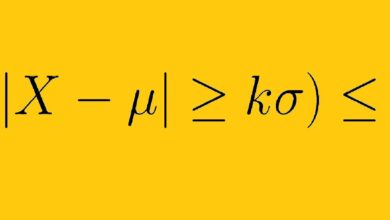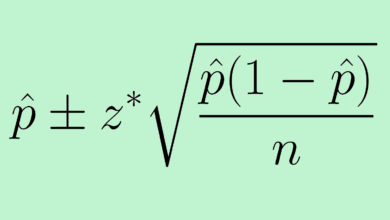
Contents
Il existe toute une série de statistiques descriptives. Des chiffres tels que la moyenne, la médiane, le mode, l’asymétrie, l’aplatissement, l’écart-type, le premier et le troisième quartiles, pour n’en citer que quelques-uns, nous renseignent sur nos données. Plutôt que d’examiner ces statistiques descriptives individuellement, il est parfois utile de les combiner pour obtenir un tableau complet. Dans cette optique, le résumé en cinq chiffres est un moyen pratique de combiner cinq statistiques descriptives.
Quels sont les cinq chiffres ?
Il est clair que notre résumé doit comporter cinq chiffres, mais lesquels ? Les chiffres choisis doivent nous aider à connaître le centre de nos données, ainsi que la répartition des points de données. Dans cette optique, le résumé à cinq chiffres se compose de ce qui suit :
- Le minimum – c’est la plus petite valeur de notre ensemble de données.
- Le premier quartile – ce nombre est désigné par Q1 et 25% de nos données se situent en dessous du premier quartile.
- La médiane – c’est le point médian des données. 50 % de toutes les données se situent en dessous de la médiane.
- Le troisième quartile – ce chiffre est désigné par Q3 et 75% de nos données se situent en dessous du troisième quartile.
- Le maximum – c’est la valeur la plus importante de notre ensemble de données.
La moyenne et l’écart-type peuvent également être utilisés ensemble pour exprimer le centre et la propagation d’un ensemble de données. Toutefois, ces deux statistiques sont susceptibles de présenter des valeurs aberrantes. La médiane, le premier quartile et le troisième quartile ne sont pas aussi fortement influencés par les valeurs aberrantes.
Un exemple
Compte tenu de l’ensemble des données suivantes, nous présenterons le résumé des cinq chiffres :
1, 2, 2, 3, 4, 6, 6, 7, 7, 7, 8, 11, 12, 15, 15, 15, 17, 17, 18, 20
Il y a un total de vingt points dans l’ensemble de données. La médiane est donc la moyenne des dixième et onzième valeurs des données ou :
(7 + 8)/2 = 7.5.
La médiane de la moitié inférieure des données constitue le premier quartile. La moitié inférieure l’est :
1, 2, 2, 3, 4, 6, 6, 7, 7, 7
Nous calculons doncQ1= (4 + 6)/2 = 5.
La médiane de la moitié supérieure de l’ensemble de données initial constitue le troisième quartile. Nous devons trouver la médiane de :
8, 11, 12, 15, 15, 15, 17, 17, 18, 20
Nous calculons doncQ3= (15 + 15)/2 = 15.
Nous rassemblons tous les résultats ci-dessus et signalons que le résumé à cinq chiffres pour l’ensemble des données ci-dessus est 1, 5, 7,5, 12, 20.
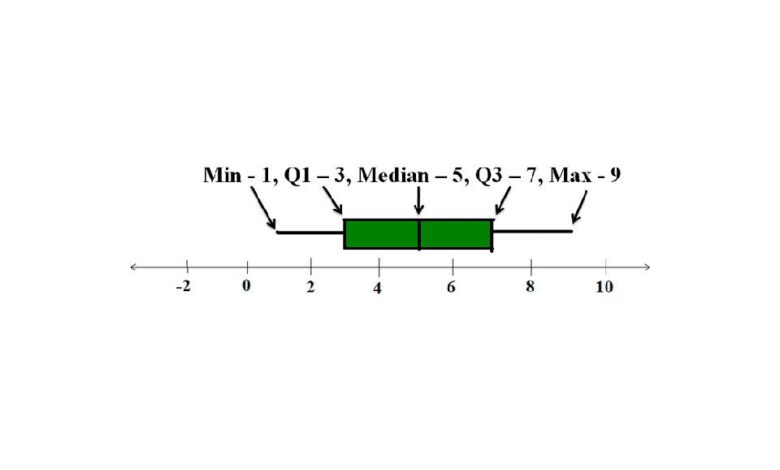
Représentation graphique
Cinq résumés de chiffres peuvent être comparés entre eux. Nous constaterons que deux ensembles ayant des moyennes et des écarts-types similaires peuvent avoir des résumés de cinq nombres très différents. Pour comparer facilement deux résumés de cinq nombres en un coup d’œil, nous pouvons utiliser un boxplot, ou un graphique en boîtes et moustaches.