Une introduction de base mais complète

Il s’agit d’une introduction de base, bien que nous l’espérons assez complète, au travail avec les vecteurs. Les vecteurs se manifestent de manières très diverses, du déplacement, de la vitesse et de l’accélération aux forces et aux champs. Cet article est consacré aux mathématiques des vecteurs ; leur application dans des situations spécifiques sera abordée ailleurs.

Vecteurs et cicatrices

Une quantité vectorielle, ou vecteur, fournit des informations non seulement sur la magnitude mais aussi sur la direction de la quantité. Lorsqu’on donne des indications sur une maison, il ne suffit pas de dire qu’elle est à 10 miles de distance, mais la direction de ces 10 miles doit également être fournie pour que l’information soit utile. Les variables qui sont des vecteurs seront indiquées par une variable en gras, bien qu’il soit courant de voir des vecteurs désignés par de petites flèches au-dessus de la variable.

Tout comme nous ne disons pas que l’autre maison est à -10 miles, la magnitude d’un vecteur est toujours un nombre positif, ou plutôt la valeur absolue de la « longueur » du vecteur (bien que la quantité ne soit pas une longueur, elle peut être une vitesse, une accélération, une force, etc.

Dans les exemples ci-dessus, la distance est la quantité scalaire (10 miles) mais le déplacement est la quantité vectorielle (10 miles au nord-est). De même, la vitesse est une quantité scalaire tandis que la vitesse est une quantité vectorielle.

Un vecteur unitaire est un vecteur qui a une magnitude de un. Un vecteur représentant un vecteur unitaire est généralement aussi en gras, bien qu’il ait un carat (^) au-dessus pour indiquer la nature de l’unité de la variable. Le vecteur unitaire xLorsqu’il est écrit avec un carat, il est généralement lu comme « x-hat » car le carat ressemble à un chapeau sur la variable.

Le vecteur zéro, ou vecteur nul, est un vecteur d’une magnitude de zéro. Il s’écrit 0 dans cet article.

Composantes vectorielles

Les vecteurs sont généralement orientés sur un système de coordonnées, dont le plus populaire est le plan cartésien bidimensionnel. Le plan cartésien a un axe horizontal appelé x et un axe vertical appelé y. Certaines applications avancées des vecteurs en physique nécessitent l’utilisation d’un espace tridimensionnel, dans lequel les axes sont x, y et z. Cet article traitera principalement du système bidimensionnel, bien que les concepts puissent être étendus avec un certain soin aux trois dimensions sans trop de difficultés.

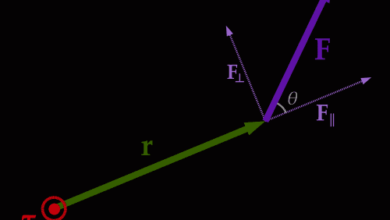
Les vecteurs dans les systèmes de coordonnées multidimensionnels peuvent être décomposés en leurs vecteurs composants. Dans le cas bidimensionnel, cela donne une composante x et une composante y. Lorsqu’on décompose un vecteur en ses composantes, le vecteur est une somme des composantes :

F = Fx Fy

thetaFxFyF

Fx / F = cos theta et Fy / F = sin thetaqui nous donneFx = F cos theta et Fy = F sin theta

Notez que les chiffres indiqués ici sont les magnitudes des vecteurs. Nous connaissons la direction des composantes, mais nous essayons de trouver leur magnitude, donc nous supprimons les informations directionnelles et effectuons ces calculs scalaires pour déterminer la magnitude. D’autres applications de la trigonométrie peuvent être utilisées pour trouver d’autres relations (comme la tangente) entre certaines de ces quantités, mais je pense que cela suffit pour l’instant.

Pendant de nombreuses années, les seules mathématiques qu’un élève apprend sont les mathématiques scalaires. Si vous parcourez 5 miles au nord et 5 miles à l’est, vous avez déjà parcouru 10 miles. L’ajout de quantités scalaires ignore toute information sur les directions.

Les vecteurs sont manipulés de manière quelque peu différente. La direction doit toujours être prise en compte lors de leur manipulation.

Ajout de composantes

Lorsque vous ajoutez deux vecteurs, c’est comme si vous preniez les vecteurs et les placiez bout à bout et que vous créiez un nouveau vecteur allant du point de départ au point d’arrivée. Si les vecteurs ont la même direction, alors cela signifie simplement qu’il faut ajouter les magnitudes, mais s’ils ont des directions différentes, cela peut devenir plus complexe.

Vous ajoutez des vecteurs en les décomposant en leurs composants, puis en ajoutant les composants, comme ci-dessous :

a b = cax ay bx par =( ax bx) + ( ay par) = cx cy

Les deux composantes x donneront la composante x de la nouvelle variable, tandis que les deux composantes y donneront la composante y de la nouvelle variable.

Propriétés de l’addition de vecteurs

L’ordre dans lequel vous ajoutez les vecteurs n’a pas d’importance. En fait, plusieurs propriétés de l’addition scalaire s’appliquent à l’addition des vecteurs :

Propriété de l’identité du vecteur Additiona 0 = aPropriété inverse de l’addition de vecteursa + –a = a – a = 0Propriété réfléchissante de l’addition de vecteursa = aPropriété commutative de l’addition de vecteursa b = b aPropriété associative de l’addition de vecteurs(a b) c = a + (b c)Propriété transitoire de l’addition de vecteursSi a = b et c = balors a = c

L’opération la plus simple que l’on puisse effectuer sur un vecteur est de le multiplier par un scalaire. Cette multiplication scalaire modifie l’amplitude du vecteur. En d’autres termes, elle rend le vecteur plus long ou plus court.

En multipliant par un scalaire négatif, le vecteur résultant sera dirigé dans la direction opposée.

Le produit scalaire de deux vecteurs est un moyen de les multiplier ensemble pour obtenir une quantité scalaire. Cela s’écrit comme une multiplication des deux vecteurs, avec un point au milieu qui représente la multiplication. C’est pourquoi on l’appelle souvent le produit scalaire de deux vecteurs.

Pour calculer le produit scalaire de deux vecteurs, on considère l’angle entre eux. En d’autres termes, s’ils partageaient le même point de départ, quelle serait la mesure de l’angle (thêta) entre eux. Le produit scalaire est défini comme suit :

a * b = ab cos theta

ababba

Dans le cas où les vecteurs sont perpendiculaires (ou thêta = 90 degrés), cos thêta sera égal à zéro. Par conséquent, le produit des points des vecteurs perpendiculaires est toujours égal à zéro. Lorsque les vecteurs sont parallèles (ou thêta = 0 degré), cos thêta est égal à 1, donc le produit scalaire est juste le produit des amplitudes.

Ces petits faits peuvent être utilisés pour prouver que, si vous connaissez les composants, vous pouvez éliminer entièrement le besoin de thêta avec l’équation (bidimensionnelle) :

a * b = ax bx + ay by

Le produit vectoriel est écrit sous la forme a x bet est généralement appelé le produit croisé de deux vecteurs. Dans ce cas, nous multiplions les vecteurs et au lieu d’obtenir une quantité scalaire, nous obtiendrons une quantité vectorielle. C’est le plus délicat des calculs vectoriels dont nous allons nous occuper, car il s’agit de pas commutative et implique l’utilisation de la redoutable règle de la main droite, que j’aborderai sous peu.

Calcul de l’ampleur

Là encore, nous considérons deux vecteurs tirés du même point, avec l’angle thêta entre eux. Nous prenons toujours le plus petit angle, donc le thêta sera toujours dans une fourchette de 0 à 180 et le résultat ne sera donc jamais négatif. L’amplitude du vecteur résultant est déterminée comme suit :

Si c = a x b, puis c = ab sin theta

Le produit vectoriel des vecteurs parallèles (ou antiparallèles) est toujours égal à zéro

Direction du vecteur

Le produit vectoriel sera perpendiculaire au plan créé à partir de ces deux vecteurs. Si vous imaginez le plan comme étant plat sur une table, la question est de savoir si le vecteur résultant va vers le haut (notre « sortie » de la table, de notre point de vue) ou vers le bas (ou « l’entrée » de la table, de notre point de vue).

La redoutable règle de la main droite

Pour le savoir, vous devez appliquer ce que l’on appelle la règle de la main droite. Lorsque j’ai étudié la physique à l’école, je détestais la règle de la main droite. Chaque fois que je l’utilisais, je devais sortir le livre pour voir comment il fonctionnait. J’espère que ma description sera un peu plus intuitive que celle qui m’a été présentée.

Si vous avez a x b vous placerez votre main droite sur la longueur de b afin que vos doigts (sauf le pouce) puissent se courber pour pointer a. En d’autres termes, vous essayez en quelque sorte de faire l’angle thêta entre la paume et quatre doigts de votre main droite. Le pouce, dans ce cas, se tiendra droit (ou hors de l’écran, si vous essayez de le faire jusqu’à l’ordinateur). Vos articulations seront approximativement alignées avec le point de départ des deux vecteurs. La précision n’est pas essentielle, mais je veux que vous compreniez l’idée puisque je n’ai pas d’image à fournir.

Si, toutefois, vous envisagez b x avous ferez le contraire. Vous mettrez votre main droite a et pointer du doigt b. Si vous essayez de le faire sur l’écran de l’ordinateur, vous vous apercevrez que c’est impossible, alors faites appel à votre imagination. Vous constaterez que, dans ce cas, votre pouce imaginatif est dirigé vers l’écran de l’ordinateur. C’est la direction du vecteur résultant.

La règle de droite montre la relation suivante :

a x b = – b x a

cabc

cx = ay bz – az bycy = az bx – ax bzcz = ax by – ay bx

abcxcyc

Derniers mots

À des niveaux plus élevés, les vecteurs peuvent devenir extrêmement complexes à travailler. Des cours entiers au collège, comme l’algèbre linéaire, consacrent beaucoup de temps aux matrices (que j’ai gentiment évité dans cette introduction), aux vecteurs et aux espaces vectoriels. Ce niveau de détail dépasse la portée de cet article, mais cela devrait fournir les bases nécessaires à la plupart des manipulations de vecteurs qui sont effectuées dans les cours de physique. Si vous avez l’intention d’étudier la physique de manière plus approfondie, vous serez initié aux concepts vectoriels plus complexes au fur et à mesure de votre formation.