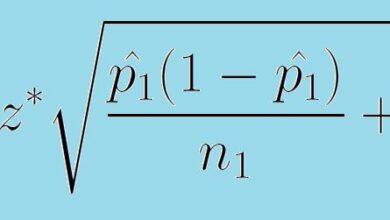Contents
La statistique inférentielle tire son nom de ce qui se passe dans cette branche de la statistique. Plutôt que de simplement décrire un ensemble de données, la statistique inférentielle cherche à déduire quelque chose sur une population à partir d’un échantillon statistique. Un objectif spécifique de la statistique inférentielle consiste à déterminer la valeur d’un paramètre inconnu de la population. La plage de valeurs que nous utilisons pour estimer ce paramètre s’appelle un intervalle de confiance.
La forme d’un intervalle de confiance
Un intervalle de confiance se compose de deux parties. La première partie est l’estimation du paramètre de population. Nous obtenons cette estimation en utilisant un échantillon aléatoire simple. À partir de cet échantillon, nous calculons la statistique qui correspond au paramètre que nous souhaitons estimer. Par exemple, si nous nous intéressions à la taille moyenne de tous les élèves de première année aux États-Unis, nous utiliserions un échantillon aléatoire simple d’élèves américains de première année, nous les mesurerions tous et nous calculerions ensuite la taille moyenne de notre échantillon.
La deuxième partie d’un intervalle de confiance est la marge d’erreur. Elle est nécessaire car notre estimation seule peut être différente de la valeur réelle du paramètre de population. Afin de tenir compte d’autres valeurs potentielles du paramètre, nous devons produire une série de chiffres. C’est ce que fait la marge d’erreur, et chaque intervalle de confiance est de la forme suivante :
Estimation ± marge d’erreur
L’estimation se trouve au centre de l’intervalle, puis nous soustrayons et ajoutons la marge d’erreur de cette estimation pour obtenir une plage de valeurs pour le paramètre.
Niveau de confiance
À chaque intervalle de confiance est associé un niveau de confiance. Il s’agit d’une probabilité ou d’un pourcentage qui indique le degré de certitude que l’on doit attribuer à notre intervalle de confiance. Si tous les autres aspects d’une situation sont identiques, plus le niveau de confiance est élevé, plus l’intervalle de confiance est large.
Ce niveau de confiance peut entraîner une certaine confusion. Il ne s’agit pas d’une déclaration concernant la procédure d’échantillonnage ou la population. Il donne plutôt une indication sur le succès du processus de construction d’un intervalle de confiance. Par exemple, des intervalles de confiance avec un niveau de confiance de 80 % ne permettront pas, à long terme, de connaître le véritable paramètre de la population une fois sur cinq.
Tout nombre compris entre zéro et un pourrait, en théorie, être utilisé pour un niveau de confiance. En pratique, 90 %, 95 % et 99 % sont des niveaux de confiance courants.
Marge d’erreur
La marge d’erreur d’un niveau de confiance est déterminée par un certain nombre de facteurs. Nous pouvons le constater en examinant la formule de la marge d’erreur. Une marge d’erreur est de la forme :
Marge d’erreur = (Statistiques pour le niveau de confiance) * (Écart-type/erreur)
La statistique relative au niveau de confiance dépend de la distribution de probabilité utilisée et du niveau de confiance choisi. Par exemple, si Cis est notre niveau de confiance et que nous travaillons avec une distribution normale, alors C est l’aire sous la courbe entre -z* et z*. Ce nombre z* est le nombre dans notre formule de marge d’erreur.
Écart type ou erreur type
L’autre terme nécessaire dans notre marge d’erreur est l’écart type ou l’erreur type. L’écart-type de la distribution avec laquelle nous travaillons est ici préféré. Cependant, les paramètres de la population sont généralement inconnus. Ce chiffre n’est généralement pas disponible lors de la formation des intervalles de confiance dans la pratique.
Pour faire face à cette incertitude quant à la connaissance de l’écart type, nous utilisons plutôt l’erreur type. L’erreur standard qui correspond à un écart-type est une estimation de cet écart-type. Ce qui rend l’erreur standard si puissante, c’est qu’elle est calculée à partir de l’échantillon aléatoire simple qui est utilisé pour calculer notre estimation. Aucune information supplémentaire n’est nécessaire car l’échantillon effectue toute l’estimation pour nous.
Différents intervalles de confiance
Il existe une variété de situations différentes qui nécessitent des intervalles de confiance. Ces intervalles de confiance sont utilisés pour estimer un certain nombre de paramètres différents. Bien que ces aspects soient différents, tous ces intervalles de confiance sont unis par le même format global. Certains intervalles de confiance courants sont ceux qui concernent une moyenne de population, une variance de population, une proportion de population, la différence de deux moyennes de population et la différence de deux proportions de population.