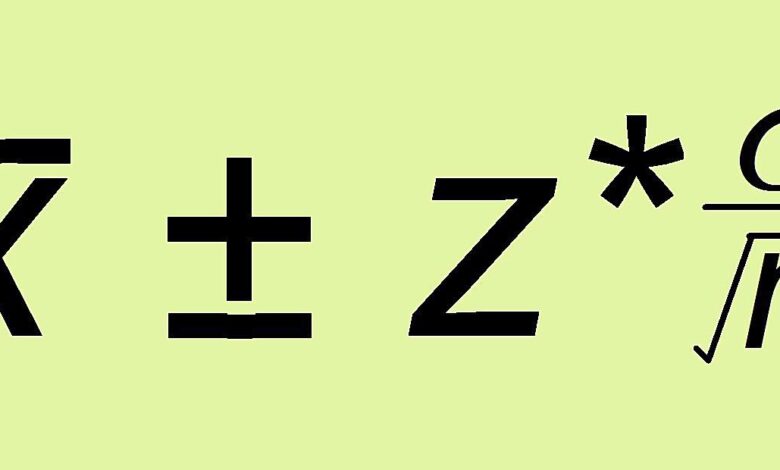
Contents
Dans les statistiques inférentielles, l’un des principaux objectifs est d’estimer un paramètre de population inconnu. Vous commencez par un échantillon statistique, et à partir de celui-ci, vous pouvez déterminer une plage de valeurs pour le paramètre. Cette plage de valeurs s’appelle un intervalle de confiance.
Intervalles de confiance
Les intervalles de confiance sont tous semblables les uns aux autres à quelques égards. Tout d’abord, de nombreux intervalles de confiance bilatéraux ont la même forme :
Estimation ± marge d’erreur
Deuxièmement, les étapes de calcul des intervalles de confiance sont très similaires, quel que soit le type d’intervalle de confiance que vous essayez de trouver. Le type spécifique d’intervalle de confiance qui sera examiné ci-dessous est un intervalle de confiance bilatéral pour une moyenne de population lorsque vous connaissez l’écart-type de la population. Par ailleurs, supposez que vous travaillez avec une population qui est normalement distribuée.
Intervalle de confiance pour une moyenne avec un sigma connu
Vous trouverez ci-dessous un processus permettant de trouver l’intervalle de confiance souhaité. Bien que toutes les étapes soient importantes, la première l’est tout particulièrement :
- Vérifier les conditions: Commencez par vous assurer que les conditions de votre intervalle de confiance sont remplies. Supposez que vous connaissez la valeur de l’écart type de la population, désigné par la lettre grecque sigma σ. Supposez également une distribution normale.
- Calculer l’estimation: Estimer le paramètre de population – dans ce cas, la moyenne de la population – en utilisant une statistique qui, dans ce problème, est la moyenne de l’échantillon. Il s’agit de former un échantillon aléatoire simple à partir de la population. Parfois, vous pouvez supposer que votre échantillon est un échantillon aléatoire simple, même s’il ne répond pas à la définition stricte.
- Valeur critique: Obtenez la valeur critique z* qui correspond à votre niveau de confiance. Ces valeurs sont trouvées en consultant un tableau de z-scores ou en utilisant le logiciel. Vous pouvez utiliser un tableau de z-score car vous connaissez la valeur de l’écart type de la population et vous supposez que la population est normalement distribuée. Les valeurs critiques communes sont 1,645 pour un niveau de confiance de 90 %, 1,960 pour un niveau de confiance de 95 % et 2,576 pour un niveau de confiance de 99 %.
- Marge d’erreur: Calculez la marge d’erreur z* σ /√n, où n est la taille de l’échantillon aléatoire simple que vous avez formé.
- Conclure: Terminez en rassemblant l’estimation et la marge d’erreur. Celle-ci peut être exprimée soit sous la forme Estimation ± marge d’erreur, soit sous la forme Estimation – marge d’erreur à l’estimation + marge d’erreur. Veillez à indiquer clairement le niveau de confiance qui est attaché à votre intervalle de confiance.
Exemple
Pour voir comment vous pouvez construire un intervalle de confiance, prenez un exemple. Supposons que vous sachiez que les scores de QI de tous les nouveaux étudiants de première année sont normalement distribués avec un écart-type de 15. Vous avez un échantillon aléatoire simple de 100 étudiants de première année, et le score moyen de QI pour cet échantillon est de 120. Trouvez un intervalle de confiance de 90 % pour le score moyen de QI de l’ensemble des nouveaux étudiants de première année.
Suivez les étapes décrites ci-dessus :
- Vérifier les conditions: Les conditions sont remplies depuis qu’on vous a dit que l’écart type de la population est de 15 et que vous avez affaire à une distribution normale.
- Calculer l’estimation: On vous a dit que vous avez un échantillon aléatoire simple de taille 100. Le QI moyen de cet échantillon est de 120, c’est donc votre estimation.
- Valeur critique: La valeur critique pour le niveau de confiance de 90 % est donnée par z* = 1,645.
- Marge d’erreur: Utilisez la formule de la marge d’erreur et obtenez une erreur de z* σ /√n = (1,645)(15) /√(100) = 2,467.
- Conclure: Concluez en rassemblant tout. Un intervalle de confiance à 90 % pour le score moyen de QI de la population est de 120 ± 2,467. Vous pouvez également indiquer cet intervalle de confiance comme étant compris entre 117,5325 et 122,4675.
Considérations pratiques
Les intervalles de confiance du type ci-dessus ne sont pas très réalistes. Il est très rare de connaître l’écart-type de la population mais de ne pas connaître la moyenne de la population. Il existe des moyens de supprimer cette hypothèse irréaliste.
Bien que vous ayez supposé une distribution normale, cette hypothèse n’a pas besoin de tenir. De beaux échantillons, qui ne présentent pas de forte asymétrie ou qui ont des valeurs aberrantes, ainsi qu’un échantillon suffisamment grand, vous permettent d’invoquer le théorème de la limite centrale. Par conséquent, vous êtes justifié d’utiliser un tableau de scores z, même pour les populations qui ne sont pas normalement distribuées.