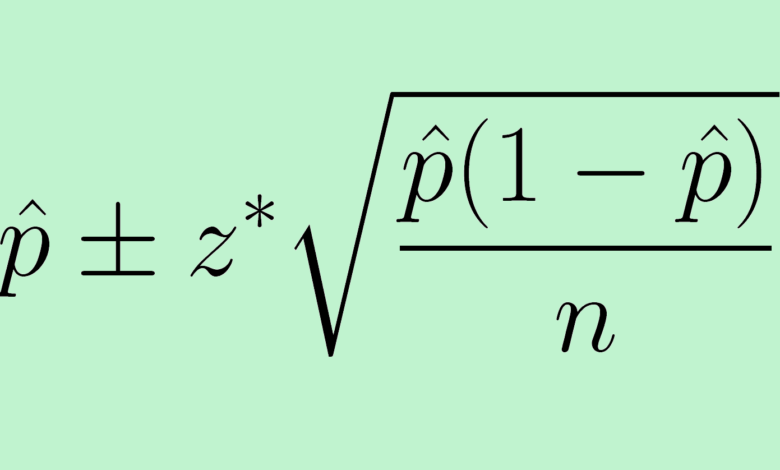
Contents
Les intervalles de confiance peuvent être utilisés pour estimer plusieurs paramètres de la population. Un type de paramètre qui peut être estimé à l’aide de statistiques inférentielles est la proportion de la population. Par exemple, on peut vouloir connaître le pourcentage de la population américaine qui soutient un texte de loi particulier. Pour ce type de question, nous devons trouver un intervalle de confiance.
Dans cet article, nous verrons comment construire un intervalle de confiance pour une proportion de la population, et nous examinerons certaines des théories sous-jacentes.
Cadre général
Nous commençons par examiner la situation dans son ensemble avant d’entrer dans les détails. Le type d’intervalle de confiance que nous allons examiner est de la forme suivante :
Estimation +/- Marge d’erreur
Cela signifie qu’il y a deux chiffres que nous devrons déterminer. Ces valeurs sont une estimation du paramètre souhaité, ainsi que de la marge d’erreur.
Conditions
Avant d’effectuer un test ou une procédure statistique, il est important de s’assurer que toutes les conditions sont remplies. Pour un intervalle de confiance pour une proportion de la population, nous devons nous assurer que les conditions suivantes sont remplies :
- Nous disposons d’un échantillon aléatoire simple de taille n provenant d’une grande population
- Nos individus ont été choisis indépendamment les uns des autres.
- Notre échantillon compte au moins 15 succès et 15 échecs.
Si le dernier élément n’est pas satisfait, il est possible d’ajuster légèrement notre échantillon et d’utiliser un intervalle de confiance de plus quatre. Dans ce qui suit, nous supposerons que toutes les conditions ci-dessus sont remplies.
Proportions de l’échantillon et de la population
Nous commençons par l’estimation de la proportion de notre population. Tout comme nous utilisons une moyenne d’échantillon pour estimer une moyenne de population, nous utilisons une proportion d’échantillon pour estimer une proportion de population. La proportion de la population est un paramètre inconnu. La proportion de l’échantillon est une statistique. Cette statistique est obtenue en comptant le nombre de succès dans notre échantillon, puis en le divisant par le nombre total d’individus dans l’échantillon.
La proportion de la population est désignée par p et s’explique d’elle-même. La notation de la proportion de l’échantillon est un peu plus explicite. Nous désignons une proportion de l’échantillon par p̂, et nous lisons ce symbole comme « p-hat » parce qu’il ressemble à la lettre p avec un chapeau sur le dessus.
Cela devient la première partie de notre intervalle de confiance. L’estimation de p est p̂.
Distribution de l’échantillon de la proportion de l’échantillon
Pour déterminer la formule de la marge d’erreur, nous devons réfléchir à la répartition de l’échantillon de p̂. Nous devrons connaître la moyenne, l’écart type et la distribution particulière avec laquelle nous travaillons.
La distribution d’échantillonnage de p̂ est une distribution binomiale avec une probabilité de succès p et n essais. Ce type de variable aléatoire a une moyenne de p et un écart-type de (p(1 – p)/n)0,5. Cela pose deux problèmes.
Le premier problème est qu’une distribution binomiale peut être très délicate à utiliser. La présence de factoriels peut conduire à des nombres très importants. C’est là que les conditions nous aident. Tant que nos conditions sont remplies, nous pouvons estimer la distribution binomiale avec la distribution normale standard.
Le deuxième problème est que l’écart-type de p̂ utilise p dans sa définition. Le paramètre de population inconnu doit être estimé en utilisant ce même paramètre comme marge d’erreur. Ce raisonnement circulaire est un problème qui doit être résolu.
La solution à cette énigme consiste à remplacer l’écart-type par son erreur-type. Les erreurs standard sont basées sur des statistiques, et non sur des paramètres. Une erreur standard est utilisée pour estimer un écart type. Ce qui fait l’intérêt de cette stratégie est que nous n’avons plus besoin de connaître la valeur du paramètre p.
Formule
Pour utiliser l’erreur standard, nous remplaçons le paramètre inconnu p par la statistique p̂. Le résultat est la formule suivante pour un intervalle de confiance pour une proportion de la population :
p̂ +/- z* (p̂(1 – p̂)/n)0.5.
Ici, la valeur de z* est déterminée par notre niveau de confiance C. Pour la distribution normale standard, exactement C pour cent de la distribution normale standard se situe entre -z* et z*. Les valeurs communes de z* comprennent 1,645 pour un niveau de confiance de 90 % et 1,96 pour un niveau de confiance de 95 %.
Exemple
Voyons comment cette méthode fonctionne à l’aide d’un exemple. Supposons que nous souhaitions connaître avec 95 % de confiance le pourcentage de l’électorat d’un comté qui s’identifie comme démocrate. Nous réalisons un simple échantillon aléatoire de 100 personnes dans ce comté et nous constatons que 64 d’entre elles s’identifient comme démocrates.
Nous constatons que toutes les conditions sont remplies. L’estimation de notre proportion de population est de 64/100 = 0,64. C’est la valeur de la proportion de l’échantillon p̂, et c’est le centre de notre intervalle de confiance.
La marge d’erreur est constituée de deux éléments. La première est z*. Comme nous l’avons dit, pour un niveau de confiance de 95%, la valeur de z* = 1,96.
L’autre partie de la marge d’erreur est donnée par la formule (p̂(1 – p̂)/n)0.5. Nous fixons p̂ = 0,64 et calculons = l’erreur type à (0,64(0,36)/100)0,5 = 0,048.
Nous multiplions ces deux nombres ensemble et obtenons une marge d’erreur de 0,09408. Le résultat final est :
0.64 +/- 0.09408,
ou nous pouvons réécrire cela comme 54,592 % à 73,408 %. Ainsi, nous sommes convaincus à 95 % que la véritable proportion de démocrates dans la population se situe quelque part dans la fourchette de ces pourcentages. Cela signifie qu’à long terme, notre technique et notre formule permettront d’obtenir la proportion de population de 95 % du temps.
Idées connexes
Il existe un certain nombre d’idées et de sujets qui sont liés à ce type d’intervalle de confiance. Par exemple, nous pourrions effectuer un test d’hypothèse concernant la valeur de la proportion de la population. Nous pourrions également comparer deux proportions de deux populations différentes.