Calculer le couple à l’aide d’exemples

Lorsque l’on étudie la façon dont les objets tournent, il devient rapidement nécessaire de comprendre comment une force donnée entraîne une modification du mouvement de rotation. La tendance d’une force à provoquer ou à modifier un mouvement de rotation est appelée couple, et c’est l’un des concepts les plus importants à comprendre pour résoudre les situations de mouvement de rotation.

La signification du couple

Le couple (également appelé moment – surtout par les ingénieurs) est calculé en multipliant la force et la distance. Les unités SI de couple sont les newton-mètres, ou N*m (même si ces unités sont les mêmes que les Joules, le couple n’est pas du travail ou de l’énergie, il ne devrait donc s’agir que de newton-mètres).

Dans les calculs, le couple est représenté par la lettre grecque tau : τ.

Le couple est une grandeur vectorielle, c’est-à-dire qu’il a à la fois une direction et une magnitude. C’est honnêtement l’une des parties les plus délicates du travail avec le couple car il est calculé à l’aide d’un produit vectoriel, ce qui signifie que vous devez appliquer la règle de la droite. Dans ce cas, prenez votre main droite et enroulez les doigts de votre main dans le sens de la rotation provoquée par la force. Le pouce de votre main droite pointe maintenant dans la direction du vecteur couple. (Cela peut parfois sembler un peu idiot, car vous tenez votre main en l’air et faites de la pantomime pour trouver le résultat d’une équation mathématique, mais c’est la meilleure façon de visualiser la direction du vecteur).

La formule du vecteur qui donne le vecteur de couple τ est :

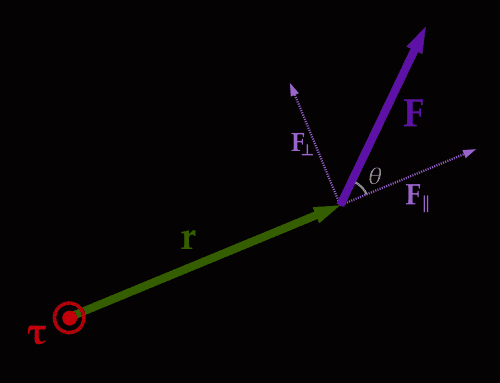
τ = r × F

Le vecteur r est le vecteur de position par rapport à une origine sur l’axe de rotation (Cet axe est le τ sur le graphique). C’est un vecteur dont la magnitude correspond à la distance à partir de laquelle la force est appliquée sur l’axe de rotation. Il pointe de l’axe de rotation vers le point où la force est appliquée.

L’amplitude du vecteur est calculée sur la base de θ, qui est la différence d’angle entre r et Fen utilisant la formule :

τ = rFsin(θ)

Cas particuliers de couple

Quelques points clés sur l’équation ci-dessus, avec quelques valeurs de référence de θ :

• θ = 0° (ou 0 radians) – Le vecteur de force est orienté dans la même direction que r. Comme vous pouvez le deviner, il s’agit d’une situation où la force ne provoque aucune rotation autour de l’axe… et les mathématiques le confirment. Puisque sin(0) = 0, cette situation se traduit par τ = 0.
• θ = 180° (ou π radians) – C’est une situation où le vecteur force pointe directement sur r. Là encore, le fait de se déplacer vers l’axe de rotation ne va pas non plus provoquer de rotation et, une fois encore, les mathématiques confirment cette intuition. Puisque sin(180°) = 0, la valeur du couple est à nouveau τ = 0.
• θ = 90° (ou π/2 radians) – Ici, le vecteur force est perpendiculaire au vecteur position. Cela semble être le moyen le plus efficace de pousser sur l’objet pour obtenir une augmentation de la rotation, mais les mathématiques le permettent-elles ? Eh bien, sin(90°) = 1, qui est la valeur maximale que la fonction sinusoïdale peut atteindre, ce qui donne un résultat de τ = rF. En d’autres termes, une force appliquée à n’importe quel autre angle fournirait un couple moins important que lorsqu’elle est appliquée à 90 degrés.
• Le même argument que ci-dessus s’applique aux cas de θ = -90° (ou -π/2 radians), mais avec une valeur de sin(-90°) = -1 entraînant le couple maximal dans la direction opposée.

Exemple de couple

Prenons un exemple où vous appliquez une force verticale vers le bas, comme lorsque vous essayez de desserrer les écrous de roue d’un pneu à plat en marchant sur la clé de roue. Dans cette situation, l’idéal est que la clé soit parfaitement horizontale, de manière à pouvoir marcher sur son extrémité et obtenir le couple maximal. Malheureusement, cela ne fonctionne pas. Au lieu de cela, la clé à ergots se monte sur les écrous de roue de manière à avoir une inclinaison de 15 % par rapport à l’horizontale. La clé à écrous a une longueur de 0,60 m jusqu’à l’extrémité, où vous appliquez votre poids total de 900 N.

Quelle est l’ampleur du couple ?

Et la direction ? En appliquant la règle « gauche-lâche, droite-serrée », vous voudrez que l’écrou de la patte tourne vers la gauche – dans le sens inverse des aiguilles d’une montre – afin de le desserrer. En utilisant votre main droite et en enroulant vos doigts dans le sens inverse des aiguilles d’une montre, le pouce dépasse. La direction du couple de serrage est donc éloignée des pneus… et c’est également la direction dans laquelle vous voulez que les écrous de roue se déplacent en fin de compte.

Pour commencer à calculer la valeur du couple, vous devez vous rendre compte que le dispositif ci-dessus comporte un point légèrement trompeur. (C’est un problème courant dans ces situations.) Notez que les 15% mentionnés ci-dessus sont l’inclinaison par rapport à l’horizontale, mais ce n’est pas l’angle θ. L’angle entre r et F doit être calculée. Il y a une inclinaison de 15° par rapport à l’horizontale plus une distance de 90° entre l’horizontale et le vecteur de force vers le bas, ce qui donne un total de 105° comme valeur de θ.

C’est la seule variable qui nécessite une configuration, donc avec cela en place, nous n’avons qu’à attribuer les valeurs des autres variables :

• θ = 105°
• r = 0,60 m
• F = 900 N

τ = rF sin(θ) =(0,60 m)(900 N)sin(105°) = 540 × 0,097 Nm = 520 Nm

Notez que la réponse ci-dessus n’impliquait que le maintien de deux chiffres significatifs, elle est donc arrondie.

Couple et accélération angulaire

Les équations ci-dessus sont particulièrement utiles lorsqu’une seule force connue agit sur un objet, mais il existe de nombreuses situations où une rotation peut être causée par une force qui ne peut pas être facilement mesurée (ou peut-être plusieurs de ces forces). Ici, le couple n’est souvent pas calculé directement, mais peut être calculé en référence à l’accélération angulaire totale, α, que subit l’objet. Cette relation est donnée par l’équation suivante :

• Στ – La somme nette de tous les couples agissant sur l’objet
• I – le moment d’inertie, qui représente la résistance de l’objet à un changement de vitesse angulaire
• α – accélération angulaire